Matasano Crypto Challenges, Set 7

Into uncharted waters we venture… this set has some various problems about famous real-world vulnerabilities, and it was challenging. fortenforge and I worked together quite a bit to get through it.

One important life pro tip: os.urandom() is BLOCKING in python. That means, even multiprocessing code will not have any speedup because of this function! Try this snippet off StackOverflow instead: bytearray(random.getrandbits(8) for _ in range(num_bytes))

Challenge 49 CBC-MAC Message Forgery

This attack emphasizes two things: that CBC-MAC should use a constant IV, and that it is vulnerable to length extension.

For the first part, the attacker controls the IV used by CBC-MAC. We want to construct a valid message of the form "from=victim&to=attacker&amount=1000". First, the attacker generates a valid message and MAC from an account that he controls (say, an accomplice), like "from=normal&to=attacker&amount=1000". Then, the attacker generates the correct IV to turn normal into victim, as follows:

evil_msg = "from=victim&to=attacker&amount=1000"
evil_padded = padPKCS7(evil_msg, 16)

# We're xoring the forged message and normal_msg to get the difference between the two, and then applying it to the iv
forged_iv = xor(evil_msg[:16], normal_msg[:16], iv)
forged_mac = CBC_MAC(key, forged_iv, evil_padded)

assert forged_mac == mac

This forged mac will now be verified by the API server.

One thing that confused me is how the attacker would be able to know the private key to communicate with the server, allowing him to construct such a message. This makes sense when the challenge explains:

[The API is] publicly exposed - the attacker can submit messages freely assuming he can forge the right MAC. The web client should allow the attacker to generate valid messages for accounts he controls. Assume the attacker is in a position to capture and inspect messages from the client to the API server.

The important thing is that the attacker can generate MACs using the private key for accounts that he controls, but not for someone else’s account.

In the second part of this challenge, the attacker uses length extension to append an evil string "attacker:10000" to a recipients list in a victim’s transaction. The attacker first generates a MAC for a valid message that names him as a recipient (say, a transaction from himself to himself). He then intercepts a normal message like "from=victim&tx_list=normaluser:1", and xors in his own message at the end, causing the resultant MAC to become his own MAC.

attacker_valid_msg = construct_message("hello", ("attacker", 10000), ("attacker", 10000))
attacker_padded = padPKCS7(attacker_valid_msg, 16)
attacker_mac = CBC_MAC(key, iv, attacker_padded)

# XOR out normal_mac to reacquire an IV of 0, then XOR in the first block of the attacker's msg
evil_msg = padded + xor(normal_mac, attacker_padded[:16]) + attacker_padded[16:]

print "C->A->S: Sending Attacker Message + MAC"
r.sendline(evil_msg)
r.sendline(attacker_mac)

Challenge 50 Hashing with CBC-MAC

This is a simple modification of the length extension of the last challenge. My evil javascript payload is an alert with a comment at the end.

forge = "alert('Ayo, the Wu is back!');//"
forge_padded = padPKCS7(forge, 16)

and, to ensure I get the same hash as the challenge snippet, 296b8d7cb78a243dda4d0a61d33bbdd1, I need to extend the CBC-MAC of the JS payload with the challenge snippet.

I can simply add a block in the middle to xor out the MAC of the payload, ensuring that the rest of the CBC-MAC is identical to the original.

concat_forge = forge_padded + xor(mac, js_padded[:16]) + js_padded[16:]

Challenge 51 Compression Ratio Side-Channel Attacks, Aka, CRIME

This has got to be the ugliest code I’ve written in a while, because my initial approach was bad…

In this challenge, we use the side channel of zlib compression to leak a session cookie in an HTTP request.

Without knowing much about the internal DEFLATE algorithm of zlib, just realize that repeated strings compress better. So, the basic idea is to bruteforce the session id by seeing whether added characters minimize the compression — telling us that the added characters are a part of the session id.

I attempt to minimize scores by adding pairs of characters, but that turned out to be unnecessary. I also utilized python’s multiprocessing library, which was also totally overkill.

pool = mp.Pool(processes = 8)
compression_lens = pool.map(compression_oracle_worker, base64_permutations)

When we are using CTR as the compression cipher, it’s pretty simple, since there’s no padding involved. Correct guesses for more characters of the id will result in lower compression lengths.

When using CBC, we have to be concerned with padding. Instead of simply minimizing the compressed length, I need to use another piece of information to determine when I’ve guessed the right characters — a padding oracle. I put in some uncompressible guess for the id and find the padding necessary to push the compressed length above a block boundary. Once I find the correct id characters, then the compressed length will be a block length (16 bytes) lower than the uncompressible guess, because I’ve compressed it below the block boundary.

The set of characters !@#$%^&*()-`~[]}{ can be used as padding, because they are not base64 characters and will not appear in the session id.

I had to do a few hacky things to get it all to work, though: I need to test two padding lengths for each guess, since my guesses are all possible pairs of base64 characters. And, python’s Pool.map doesn’t take multiple arguments, so I have to pass in a list of lists to my oracle worker.

base64_perms = [[padding[:-1], final + "".join(perm)] for perm in it.permutations(base64_chars, 2)]
base64_perms += [[padding[:-2], final + "".join(perm)] for perm in it.permutations(base64_chars, 2)]

Challenge 52 Iterated Hash Function Multicollisions

The next three challenges all involve attacks on the Merkle-Damgard hash construction. We encountered this previously with MD5 and SHA1, and we’ll be using a specifically weakened version in these challenges.

The basic idea in this challenge is that, once we find an initial collision of an iterated hash function, we can generate a ton more by extending that initial collision. The relevant paper is Joux. The key figure is .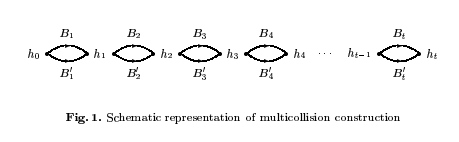

We can see that we can construct colliding messages by selecting one of $B_i$, $B_i'$ for each $i$, giving us a total of $2^i$ colliding messages. Each message has the same intermediate hash values, $h_0, h_1...$.

Now that we have a cheap way to generate collisions (if we ever need more, we can double how many collisions we have with very little work), we can break a cascaded hash function that just concatenates a weak hash and a strong hash. In my code, my “weak” hash is a Blowfish cipher truncated to 2 bytes of output, and my “strong” hash is truncated to 3 bytes of output.

We can simply search in our pool of weak hash collisions for a pair of messages that also collides in the strong hash. No luck? Then double the number of weak hash collisions (easy!) and keep looking…

Challenge 53 Kelsey and Schneier’s Expandable Messages

It took me a little bit to understand this attack. The best explanation is Schneier’s paper here..

The goal here is to break second preimage resistance — as the challenge states, finding $x'$ such that $H(x') = H(x) = y$.

Remember that, in the iterated hash function construction, if the internal hash state of two different messages are ever equal, then we can make sure that all following hash states, including the output, will be equal (by ensuring that the messages don’t differ after this point). So, if we have a very long message of $2^R - 1$ blocks, we have $2^R$ intermediate hash states that we can potentially collide with, decreasing the difficulty of finding a second preimage.

However, length padding screws this up. MD construction calls for the length of the message to be appended to the message before the final hash is output, which prevents the above attack. We are forced to find a colliding message of length $2^R - 1$! Fortunately, we can bypass this defense with expandable messages that allow us to actually construct a message of this length very easily.

We first find pairs of colliding messages, where each pair consists of a single-block message and a message of length $2^{k-1} + 1$. Each pair’s initial hash state is the colliding hash of the previous pair. This is our expandable message.

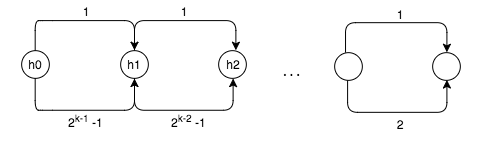
When we want to construct a message of length between $k$ and $k + 2^k - 1$, we can create it by concatenating pieces of our expandable message (you might already be able to see how if you are familiar with binary search). For each block in our chain, we can either append the single-block message or the $2^{i} - 1$ message, allowing us to build a message of any length that hashes to the same output as the others. The result will look something like this:

So, all that remains to get our second preimage is to find a single “bridge” block that will allow our expandable message to hash to one of the intermediate states of the long message. Once we find this block, which collides with the $n$th intermediate hash state of the long message, we simply produce a message of length $n$ in the manner shown above.

# Where prefix is generated from our expandable message
prefix = generate_prefix(intmed_state_hash_index)

second_preimage = prefix + linking_block
second_preimage += target_long_msg[len(second_preimage):]

Challenge 54 Kelsey and Kohno’s Nostradamus Attack

This challenge deals with another kind of preimage resistance — we want to make a prediction about some event that hashes to some output $H$, and after the event has passed, create a correct “prediction” that also hashes to $H$, thus convincing people that we knew the results of the event beforehand.

This attack is also known as the “herding” attack, and it’s easy to see why. The basic premise is to construct a “collision tree” by selecting a bunch of starting hash states, finding message blocks under which pairs of these states collide, and building up a binary tree to a root hash state. The paper calls this tree a “diamond structure”, and it’s very easy to produce.

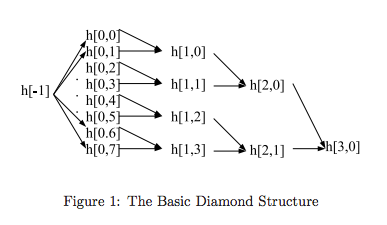
Once we have the collision tree, we can choose our prefix (the actual result of the event) and append some glue blocks so that the last one collides with one of the leaves in our tree. Then, as the challenge says “Follow the path from the leaf all the way up to the root node and build your suffix using the message blocks along the way.”

Challenge 55 MD4 Collisions

To be honest, this challenge makes everything else look like chump stuff.

fortenforge and I worked on this together for several days, and when I got tired of it, he soldiered on, ending up with a beautiful MD4 collision. I’ll refer you to his writeup in lieu of explaining it myself, and he deserves all the credit for this excellent piece of work.

Challenge 56 RC4 Single Byte biases

This seems like a pretty silly challenge, and I couldn’t get it to work. We basically trust this paper that says that the RC4 encryption function is biased towards certain bytes at certain byte positions — byte 0, 16, 32, etc. For instance, the RC4 ciphertext’s 16th byte is biased towards 0xF0. To quote the paper,

Suppose byte $Z_r$ of the RC4 keystream has a dominant bias towards value 0x00. As RC4 encryption is defined as $C_r = P_r ⊕ Z_r$, the corresponding ciphertext byte $C_r$ has a bias towards plaintext byte $P_r$. Thus, obtaining sufficiently many ciphertext samples $C_r$ for a fixed plaintext $P_r$ allows inference of $P_r$ by a majority vote: $P_r$ is equal to the value of $C_r$ that occurs most often.

Unfortunately, you need to RC4 encrypt a ton of messages under random keys for this to work, which takes a lot of time, and the results were not at all good for me, even with $2^{24}$ encryptions for each byte.

def attack_byte(idx):
        chars = {char: 0 for char in range(256)}

        padding = 'A'*(15 - idx)

        for i in range(2**20):
            if i % (10**6) == 0:
                print("Iteration: ", i)
            ctext = rc4_oracle(padding)
            guess = ctext[15] ^ 0xf0
            chars[guess]+= 1

        max_char = max(chars.items(), key = op.itemgetter(1))