Challenge 17 The CBC padding oracle!!!
The CBC padding oracle is a very famous attack. We have an oracle function that takes in a ciphertext and decrypts it, returning True if the plaintext is padded properly.
The process behind the attack on each block is:
- For each byte, starting at the last position, modify the ciphertext in the previous block, cycling through all 256 possibilities for the plaintext until I find the correct one. Here’s the explanation of how I make and check my guesses.
For the currently examined block, remember that I can modify the previous block’s ciphertext, which will be XORed with this block’s intermediate state to get a modified plaintext. What is the goal for the modified plaintext? It’s to get the proper padding bytes at the end of it!
So, to decrypt the last byte of the block, I first provide the correct offset
1 | new_ciphertext, C': |
If I cleverly choose the value of Z, then the last byte of C’, U above, will XOR to the correct padding byte, \x01.
I XOR out the corresponding byte from the ciphertext, XOR out a guess for the flag byte character, and XOR in the desired padding byte (\x01).
1 | pad_str = offset_pad + xor(prev_block[-desired_padding_byte], cand_ord, desired_padding_byte) |
I create the new_ciphertext C' by inserting my crafted block C[-2]' before the block I’m currently examining.
1 | new_ciphertext = ciphertext[:-32] + pad_str + ciphertext[-16:] |
If my guess is correct, then only \x01 will be left, and padding_oracle(new_ciphertext) will return True.
- If I’m not examining the last character in the block, then the desired padding bytes will be something greater than
\x01. I modify the following ciphertext bytes I’ve already solved to XOR out the ciphertext byte, XOR out the known flag bytes, and XOR in the desired padding byte (\x02 - \xF).
1 | pad_str = pad_str + xor(prev_block[-desired_padding_byte+1:], known_last_bytes, desired_padding_byte) if len(known_last_bytes) > 0 else pad_str |
As before, the correct guess will cause the byte of interest to XOR to the proper padding byte, and padding_oracle(new_ciphertext) will return True.
1 | new_ciphertext, C': |
Above, I want the plaintext bytes at positions UK to decrypt to \x02\x02. Modifying K to decrypt to \x02 is simple because I already know the byte and can fully control what to XOR in or out.
Note: The ‘previous ciphertext’ block for the first block is the IV, so we perform the XORs on it the same way we would modify any other block.
The wrapper function, padding_oracle_attack(padding_oracle, ciphertext, blocksize), will loop through calls to decipher_block to find the last block, append the found bytes to the flag, and on the next iteration, slice out the blocks of ciphertext I’ve already solved.
Challenge 18
This challenge is to implement CTR (Counter) stream cipher mode. CTR mode does not encrypt the plaintext — rather, it encrypts a running stream of counter bytes, which is then XORed with the plaintext.
One benefit of CTR mode is that it does not require padding.
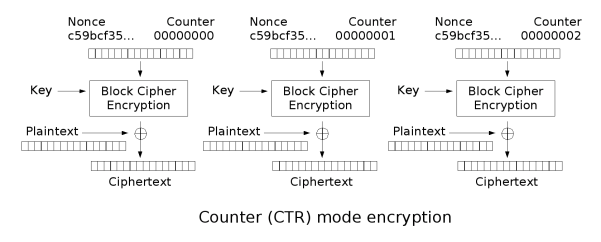
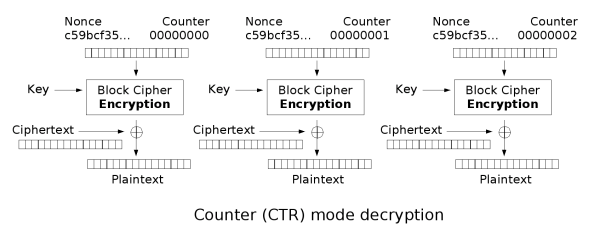
I define a CTR() class in set3_utils. Decryption is identical to encryption. In encrypt, I generate the keystream, in 128 byte chunks, for all of my plaintext, which looks like
1 | keyblock = e.update(p64(self.nonce, 'little') + p64(self.counter, 'little')) |
These are pwntools packing functions, packing the counter in little-endian format. The nonce is a random, secret value that composes the first 64 bytes of every keystream block.
After XORing my keystream with the plaintext, I save the unused keystream bytes in self.carry_over_bytes. The next time I run decrypt() or encrypt(), I set keystream = self.carry_over_bytes so I use all the bytes of previously-generated keystreams.
Challenge 19 Break fixed-nonce CTR mode using substitutions
Challenge 20 Break fixed-nonce CTR statistically
In this challenge, using a fixed-nonce for CTR will essentially boil down to solving repeating-key XOR, where the repeating-key is the reused ciphertext of the CTR keystream.
I know that each encrypted text has been XORed with the same keystream. I first pad each encrypted text with 0’s to the same length (anything longer than the longest line).
1 | padded_encrypted_texts = [text.ljust(max_length, '0') for text in encrypted_texts] |
Then, I can simply concatenate all the ciphertexts into one long string, as if a repeating-xor-key of length max_length had been applied.
1 | keystream = breakRepeatingXor("".join(padded_encrypted_texts), max_length) |
The result will be a keystream that, when XORed with each encrypted text, should produce mostly readable text. The accuracy towards the end of the longer strings will degrade, because there is not enough information to determine the correct key — there are simply not enough strings near the maximum length to determine the key based on letter frequency.
Challenge 21 Implement the MT19937 Mersenne Twister RNG
The Mersenne Twister is by far the most common PRNG (pseudo-random number generator). The most common version is based on the Mersenne prime 219937−1, and has a known set of constants and magic values.
There are three main components of MT19937, 32-bit values.
- Initialization of the first set of 624 values from a seed
- Outputting the next number from the RNG, after some tempering
- Generating a new set of 624 values (twisting)
In step 1, we initialize the self.state array by setting the first value to be the seed, and then calculating the rest from the formula off Wikipedia, x[i] = f × (x[i-1] ⊕ (x[i-1] >> (w-2))) + i, where w is the word size, 32 bits.
1 | for i in xrange(1, 624): |
where f is a magic, 1812433253.
In step 2, the RNG outputs a number by taking the next state value, indexed by self.index, and applying some temper transforms before returning it. Then, we increment self.index to use the next state value next time.
When we have used up 624 values, we “twist” to generate more.
For each state value, the RNG concats the MSB of the current state value and the other 31 bits from the next state value.
1 | y = (self.state[i] & 0x80000000) + (self.state[(i+1) % 624] & 0x7fffffff) |
Then it does the A transform above: right-shifts by one, and XORing an additional magic if the current state value is odd. We also XOR with the 397th-next former state variable.
1 | self.state[i] = self.state[(i+397) % 624] ^ (y>>1) |
1 | if y % 2 != 0: |
Challenge 22 Crack an MT19937 seed
Challenge 23 Clone an MT19937 RNG from its output
TO clone an MT19937 RNG, we need to find its 624-value internal state. We need to get 624 RNG outputs, and untemper each one.
The untempering is very tricky — remember that we did this sequence of two right shifts and two left-shift ANDs:
1 | temp ^= (temp >> 11) |
Let’s see how to undo that right shift:
1 | 10110111010111110001000011001110 ^ |
We iterate through all the bits of the output, starting from the leftmost bit
1 | for i in xrange(32): |
While i < shift, getBit() will return 0 as the XOR bit, and recovered_bit will just be the same as the output bit. When i = shift, orig_bits will contain the first shift original bits. getBit(orig_bits, i - shift) will emulate the right-shifted original value, grabbing original bit values, starting from the left of orig_bits. Thus, the XOR of the output_bit and the corresponding index of orig_bits will recover the next original bit.
1 | When i = 18 |
Note that, if shift < 16, at some point each recovered original bit is used immediately in the next iteration of the for loop to recover the next bit.
To untemper the left shift + and + xor, we reconstruct the original from the right side, not the left.
1 |
|
1 | for i in reversed(xrange(32)): |
While i + shift > 31, the undo_xor_bit is 0, so the last shift bits of orig_bits are identical to the last shift output_bits.
Once i <= 31-shift, we begin using values from the right side of orig_bits, emulating the left-shifted value. We then & in the magic bit, and XOR with the output bit to recover the next original bit.
1 | When i = 24 |
Our final untemper function is just reversing the 4 tempers,
1 | def untemper(val): |
and we can easily clone an RNG’s 624-value state:
1 | for i in xrange(624): |
We check that a MT with the cloned state does in fact generate the same numbers as the original MT. Done!
1 | cloned_mt = MT19937(arbitrary value) |
Challenge 24 Create the MT19937 stream cipher and break it
We first need to create an MT19937 stream cipher, which operates much like CTR mode. The keystream, the RNG output, is simply XORed to decrypt or encrypt.
We have an oracle that appends some random prefix to our plaintext before encrypting it using the MTR Stream cipher.
We first find the prefix length, by simply subtracting the length of the plaintext from the len of oracle-returned ciphertext — the added length in the ciphertext must be due to the prefix, since there’s no padding in a stream cipher.
1 | Step 1: |
We then iterate through all possible seed values, 1…216. We create a MT Cipher with each seed, encrypting our padded data and seeing if it gives the same ciphertext as the oracle did. (Remember to slice out the random prefix when comparing!) If the ciphertexts match, we have found our seed!
1 | for i in xrange(2**16): |
